Kurser
Tilbage til oversigtssiden.
Blok 1 - 2007
Fysik 1 laboratorieøvelsers logbog
Dette er en logbog over de øvelser der foregår under Fysik 1's frie øvelser. Eftersom logbogen er en del af selve øvelserne vil jeg her skrive alt hvad vi laver samt lægge links op til relevante sider, dokumenter samt målinger.
Opbygningen af selve logbogen er som følger: Hver torsdag hvor vi har øvelser skriver jeg op hvad vi har lavet samt hvilken gruppe jeg var i (inklusive gruppemedlemmerne). Når jeg f.eks. skriver at jeg har været i gruppe nummer 3 skal man gå ud fra at vi brugte computer nummer 3.
Normalt bruger jeg min egen bærbare i forbindelse med computeropskrivninger mm., og jeg sørger altid for selv at have målinger og andre dokumenter liggende lokalt ud over de filer der selvfølgelig ligger på den computer vi har brugt på selve dagen. Alle de relevante filer som vi har brugt den enkelte øvelsesdag vil jeg altid lægge links til i logbogen.
Uge 35 - Godkendt logbog
Logbog over første gang i lab med introduktion til computersystemet
Fysik 1, hold 3, gruppe 3
30.08.2007, torsdag formiddag
Gruppemedlemmer
Mads Bertelsen, Evan James Shymko og Pia Jensen.
Det lavede vi
Vi skulle lære computersystemet at kende og lave vores hjemmeside på fys.ku.dk serveren. Til at gøre dette fik vi en lille guide som vi skulle følge, inklusive nogle forskellige links til blandt andet en hjemmeside hvor man bare kunne kopiere kildekoden og lave sin egen hjemmeside ud fra denne.
Krav
Kravene til opgaven var at vi skulle skrive vores navn, e-mailadresse mm. på hjemmesiden, hvilket man da også kan se på min hjemmesides index.
Uge 36 - Godkendt logbog
Logbog over øvelse med skråt kast med fjederkanon
Fysik 1, hold 3, gruppe 1 og 2
06.09.2007, torsdag formiddag
Gruppemedlemmer
Simon Loftager, Tomas Palsson, Kasper Kofoed Ljungdahl, Michael Hansen og Pia Jensen.
Beskrivelse af forsøg
Vi har lavet et forsøg med en fjederkanon for at skulle bestemme mundingshastigheden.
For at gøre dette har vi skudt med kanonen hen over et bord hvorpå der var papir med carbonpapir
ovenpå så vi kunne se hvor kanonkuglen landede.
Lige nu har vi målingerne for hvor kuglen er landet som (x,y) koordinater i forhold til kanonens
munding. Disse målinger har vi for vinklerne 15, 30, 45, 60 og 75 grader.
Fejlkilder
- Vi har ikke regnet med luftmodstand.
- Kanonen hældte lidt, så vi hele tiden skød med en forkert vinkel i forhold til hvad vi regner med (vi fik en lidt for stor vinkel).
- En form for rekyl på kanonen, når man skød blev vinkelen mere vertikal end den var bestemt til at være.
Målinger
Måleusikkerheder, da vi kun har kunnet måle med plus/minus 1 mm.
Målingerne kan hentes her.
Uge 37 - Godkendt logbog
Logbog over intro til VPython
Fysik 1, hold 3, gruppe 8
13.09.2007, torsdag formiddag
Gruppemedlemmer
Mads Bertelsen, Johan Jacobsen og Pia Jensen.
Det lavede vi
Først og fremmest lavede vi en bunke opgaver om bevægelser i ovaler. Vi skulle indtegne hastigheds- og accelerationsvektorer i forskellige bevægelser med eller uden hastighedsforøgelse/sænkning og finde sammenhænge mellem vinkler og sådan noget. Til sidst skulle vi indtegne accelerationsvektorer i jævne og ikke-jævne cirkel- og peanutformede bevægelser.
Derefter fik vi udleveret en guide i hvordan man starter op med VPython, og denne skulle vi så følge slavisk fra ende til anden. Den guide vi fik har jeg smidt i et pdf-dokument som kan downloades her. (Eller som LaTEX kildekode her.)
Links vi fik
Der var lige et par links som vi fik i vejledningen som jeg vil liste op her:
- VPython.org, VPythons hovedside hvor man blandt andet kan finde guides og downloads af den nyeste version af Python og VPython.
- VPython Intro, en pdf "tutorial" hentet fra VPython.org.
Programmer lavet
Først og fremmest lavede vi vores første program, der kan hentes her. I dette program lavede vi en grøn bold der faldt nedad med en acceleration på g og tegnede en impulsvektor foran sig samt en linie bag sig hvor den havde været. Jeg har taget et screenshot af et sådant program, for at se det i fuld størrelse så klik på billedet herunder:
Vi fik desuden vist et eksempelprogram af Ian Bearden, som kan hentes her. Med dette eksempelprogram lærte vi lidt mere om hvordan man kan lave pile og linier og lidt om at man kan lave animationerne interaktive. Vi redigerede desuden en smule i eksempelprogrammet, og denne redigering kan hentes her.
Diskussion
Omkring tidsintervallet der skal bruges i VPython blev vi enige om at et tidsinterval på 0.1 s for en bold nok er fint, men ser man på partikelfysik eller store galakser er det nok lidt overkill at bruge enten så lidt eller så meget.
Uge 38 - Godkendt logbog
Logbog over intro til VPython 2
Fysik 1, hold 3, gruppe 9
20.09.2007, torsdag formiddag
Gruppemedlemmer
Malik Bistrup, Evan James Shymko og Pia Jensen.
Det lavede vi
Vi fik først og fremmest, som altid, udleveret nogle opgaver der skulle regnes. Denne gang handlede de om nogle blokke der blev skubbet og så skulle vi se på tilfælde med konstant fart og varierende fart.
Derefter skulle vi i gang med noget lidt mere avanceret VPython. Den vejledning vi fik udleveret kan hentes her (eller som LaTEX kildefil her). Denne vejledning skulle vi så følge igennem nogle forskellige nye ting med VPython - hvor vi til sidst skulle ende op med et program der illustrerede det kanonforsøg vi lavede i uge 2.
Svar på spørgsmål i løbet af opgaven
I løbet af gennemgangen af guiden var der en del spørgsmål, som jeg lige vil liste op her sammen med de svar vi i gruppen blev enige om.
- Why do I call this a particle? What role do the mass and the size as defined in your
program play?
- Det er rigtigt at kalde bolden for en partikel fordi den faktisk kun er defineret i et punkt. Selve radius for bolden definerer ikke hvor meget bolden fylder eller vejer - egenskaber som masse og densitet har bolden først hvis vi giver den det i koden.
- When might we need to use time dependent forces? If we had more than one object, would we
need to approach this differently? How?
- Tidsafhængige kræfter kunne for eksempel være ved en raket, hvor massen jo ændrer sig over tid - eller hvis man har en luftmodstand (der jo ændrer sig med hastigheden - som igen ændrer sig over tid).
- Hvis vi nu havde flere objekter som skal påvirkes af forskellige kræfter så kunne vi bare lave flere variable - men stadig beholde det ene tidsloop.
- Omkring at eksaktheden af en række målinger bliver bedre når man tager dem mange gange:
Is this also true of the results of your program? Why or why not? How would you expect the
answer you get to change if you run your program 10 times? 100 times? 1000000 times?
- Eftersom det bare er et program vi arbejder med vil der ikke være nogen forskel på nøjagtigheden om vi kører programmet en enkelt gang eller 1000000 gange for den sags skyld - programmet vil til stadighed gøre det samme igen og igen, for der er ikke noget tilfældigt i hvad en computer gør.
- How do we define the "ground"? How do we determine the position at this time?
- Vi definerer jorden som værende der hvor y-koordinaten er nul igen. I og med at vi skød bolden af sted så den var i højden 0 til tiden 0 må den også være ved højden 0 igen når den rammer "jorden". Så i VPython kan vi bare fortælle at den skal stoppe når den er ved y = 0 igen.
Programmet
Vi startede ud med det program vi sluttede med i sidste uge, dette program redigerede vi lidt så det faktisk også tog højde for at der er en acceleration i det lille tidsrum dt ved at tilføje leddet 0.5*NetA1*dt**2 i leddet for mass1.pos. Det ændrer ikke meget når vores tidsinterval er småt, men i princippet bør vi have det med.
Vi opstiller så efter guiden et udtryk for den kraft som vores partikel er påvirket af. Lige nu er den bare g, så den er nem at opstille. Herefter skulle vi så tilpasse kastet så det faktisk fungerede lige som vores kanonskud. Vi udregnede starthastigheden på en af de måleserier som vi tog under forsøget. Måden vi har udregnet det på har jeg vist her. For at kunne måle hvor langt kastet blev i x-retningen lavede vi desuden et label som udskrev x-koordinaten for partiklen. Eftersom vi fik vores partikel til at stoppe med sit fald-loop når den kom til y = 0, så stoppede den altså også med labelet hvorpå der stod kastelængden.
Herefter ville vi gerne tilføje lidt luftmodstand på vores partikel, og for at gøre dette læste
vi lidt på Wikipedia om luftmodstand, hvor vi så at luftmodstand er givet ved formelen:

Denne kraft kunne vi så bare lægge til den resulterende kraft som vi tidligere havde defineret i vores loop (ved at gange alt det andet med vores allerede definerede hastighed mass1.velocity i anden potens). Vi kunne tydeligt se hvordan bolden ikke kom nær så langt som før hvor der ikke var vindmodstand.
Tilføjelse af usikkerheder
Vores kast er selvfølgelig det samme hele tiden med mindre vi indsætter noget tilfældigt i det. Derfor tilføjer vi random til biblioteket af funktioner, og kan nu bruge gauss(meanX,sigmaX), hvor meanX er gennemsnitsværdien af gauss-fordelingen og sigmaX er bredden af den. Vi lavede så et output fra gauss-funktionen og lagde dette til vores hastighed for hver funktion - så der altså er en usikkerhed på kanonens starthastighed i alle tre dimensioner. Vi valgte meanX af gauss-fordelingen til at være 0, da vi jo lægger et tal til eller trækker det fra vores egentlige starthastighed, så i det ideelle tilfælde skulle værdien for vores usikkerhed være nul. SigmaX, spredningen, sætter vi til at være samme spredning som den vi fandt i vores forsøg i uge 36.
Vi kunne så tilføje til programmet at det skulle køre mange gange i træk og hver gang udskrive kastelængden og sluthastigheden til os i shell'en. På denne måde kunne vi se at gauss-funktionen faktisk gjorde at kastelængderne og sluthastigheden ikke var den samme hver gang.
Gode VPython kommandoer
Vi fandt ud af at man kunne ændre opløsningen på selve billedet med scene.width og
scene.height.
For at kalde et label noget fra en vektor kan man bare kalde det ene koordinat ved at skrive
vektornavn.x, y eller z.
Programmer lavet
Det første program vi lavede og legede med kan hentes her. Det andet med usikkerheder, luftmodstand og det hele kan hentes her.
Uge 39 - Godkendt logbog
Logbog over øvelse med HotWheels
Fysik 1, hold 3, gruppe 5
27.09.2007, torsdag formiddag
Gruppemedlemmer
Katrine Rasmussen, Kasper Steenstrup og Pia Jensen.
Det lavede vi
Først og fremmest lavede vi som sædvanlig først og fremmest en bunke opgaver - denne gang omhandlende kræfter og arbejde. Efter dette fik gik vi ved hjælp af følgende vejledning (download som LaTEX kildekode her) videre med at lave et forsøg med HotWheels biler i et loop.
Forsøget
Selve forsøgte gik ud på først og fremmest at udregne den teoretiske højde hvorfra vi skulle slippe en lille bil så den præcist ville kunne køre rundt i et loop uden at falde ned. Efter at vi havde udregnet den teoretiske højde skulle vi teste og denne højde nu også passede ved faktisk at tage en lille legetøjsbil på en bane med et loop.
Den teoretisk udregnede højde kan ikke være nok, da vi har set bort fra luftmodstand og gnidning. Vi fandt derfor den højde som skal til (ekstra) for at bilen kan komme igennem loopet uden at falde ned.
Optimering af forsøget
Vi prøvede så at se om denne ekstra højde ændrede sig for en bil med større masse. Dette gjorde den ikke synligt for en bil med cirka den dobbelte masse, så den gnidningsmodstand mellem bilens hjul og banen (der er afhængig af massen på bilen, da den er afhængig af normalkraften) er meget meget lille - i hvert fald i forhold til de andre kræfter vi ikke tog højde for under den teoretiske udregning.
For at se lidt mere på gnidningsmodstand testede vi hvor stor en vinkel der skulle på en banedel for at bilen kørte med tilnærmelsesvis konstant hastighed, denne vinkel var meget lille - hvilket igen siger os noget om gnidningskoefficienten - at den er meget lille.
Der kan dog også godt være en gnidningsmodstand mellem hjulene og kanterne, og denne må være større end den der er mellem hjulene og banen (da denne er statisk eftersom hjulene drejer rundt - hvilket de ikke gør i forhold til kanterne på banen). Denne gnidning har vi ikke rigtig kunnet regne på, endsige lave noget form for forsøg med det. Vi snakkede lidt om at sætte tape op mod kanterne af banen for derved at se hvordan bilens kørsel ændrede sig, men det var for svært at gøre i praksis.
Hvis man puster på bilen når den står på en banedel der ligger vandret, så skal der en del til for at bilen bevæger sig, men der skal meget mindre til end hvis bilen står på et bord der tydeligt har en større gnidningskoefficient. Dette betyder igen at der er en ret lille gnidningskoefficient mellem banen og bilens hjul (husk at denne gnidning er statisk og ikke kinetisk - eftersom bilens hjul drejer rundt og ikke glider på overfladen) - men det betyder også at luftmodstanden på bilen ikke er ekstremt stor. Den er trods alt også formet som en sportsvogn, der jo normalt er lavet til ikke at skulle give stor luftmodstand.
Måleusikkerheder
Da der er en kant på banen kan vi ikke 100 % se om bilen slipper banen eller ej, men hvis vi nu under systemet havde en meget præcis vægt ville vi i stedet for at aflæse med øjnene kunne aflæse på vægten (hvis den kunne gemme data i forhold til tid) hvornår en (tid,vægt)-kurve gav en pæn kurve med et nulpunkt, hvor normalkraften på bilen altså er nul i toppen, mens den selvfølgelig er over nul når bilen er i et andet punkt i kurven. Et billede af vores bane er at finde ved at klikke på billedet herunder:
Sammenkoblingerne i banen giver desuden også ekstra gnidning, som vi ikke rigtig kan arbejde med eftersom denne ikke engang er tilnærmelsesvist konstant i løbet af turen (der er to sammenkoblinger som bilen skal over før loopet og en enkelt sammenkobling lige når den kører ind i loopet).
Konklusion
Gnidningen mellem hjulene og banen er meget lille, mens luftmodstanden bør være lidt større eftersom hastigheden for bilen er stor (og luftmodstand er afhængig af hastighed). Derudover er der en gnidning mellem siden af hjulene og banekanten som vi ikke kan komme til at teste.
(Desuden skal vi tage højde for at bilen jo er rød, vil den bare have lyst til at køre hurtigere, hvorfor alt det andet totalt kan ignoreres da vores bil bare er sej!) Et billede af vores bil er at finde ved at klikke på billedet herunder:
Udregninger
Jeg vil tage udgangspunkt i den situation vi er blevet givet og regne ud fra denne teoretisk,
først og fremmest uden luftmodstand og gnidning. For at bilen skal blive på banen i toppen af
loopet skal centripetalaccelerationen være den samme som tyngdeaccelerationen - så er den hastighed
som bilen har i toppen af loopet givet ved:

Den kinetiske energi lige i toppen hvor vi slipper vores bil, altså i højden h, må være nul, da hastigheden her også er nul. Vi giver altså ikke bilen noget starthastighed, så al den mekaniske energi må være givet ved gravitationel potentiel energi. Denne sidste afhænger af massen m af bilen, tyngdeaccelerationskoefficienten samt den højde hvori vi slipper bilen:

I positionen i toppen af loopet vil noget af den mekaniske energi være givet ved den kinetiske energi (som igen er givet ved den hastighed som jeg tidligere fandt ud fra argumentet om at centripetalaccelerationen skulle være lig med tyngdeaccelerationen) og den gravitationelle potentielle energi i højden 2 R, hvor R er radius af loopet:

Da jeg ikke regner med at der er hverken luftmodstand eller gnidning i systemet vil min bil på min bane være et isoleret system, hvorfor der vil være energibevarelse. Dette betyder at jeg kan sætte de to mekaniske energier lig med hinanden, hvorefter jeg kan finde højden h givet ved R:

Og jeg har altså et udtryk for den højde som bilen teoretisk set skal slippes i for at den lige præcis kan komme rundt i loopet.
Det viser sig dog hurtigt at dette over hovedet ikke passer. Når vi selv udfører forsøget
ser vi at bilen, når den starter ud i den teoretiske ideelle højde h, ikke kan komme hele vejen
rundt i loopet - det har den simpelthen ikke energi nok til. Dette er selvfølgelig fordi vi ikke
tog højde for luftmodstand og gnidning i de første udregninger, og altså så systemet som
isoleret. I virkeligheden vil der være et negativt arbejde på bilen når den kører af sted, som
skyldes en kombination af alle de faktorer vi har ignoreret. Dette drejer sig altså primært
om luftmodstand og gnidning (både gnidning internt i bilen mellem dens hjul og karosseriet,
gnidning mellem hjulene og banen samt gnidning mellem kanten af hjulene og kanten af banen).
Sætter vi dette ekstra arbejde ind i vores energiligning vil vi endnu engang kunne bruge den
som energibevarelse, denne gang bare med et lidt større system:

Når vi i forsøget hæver bilen lidt ekstra op, for at se hvor langt op den skal for at den rent faktisk kan komme igennem loopet, så tilføjer vi bilen den ekstra energi der bliver taget fra den i løbet af dens tur. Selvfølgelig vil der også være en lille gnidning og en lille smule luftmodstand ekstra på det stykke ekstra som bilen skal bevæge sig når vi tager den længere op, men dette er meget lidt, hvorfor vi kan ignorere det. Vi har altså et udtryk for det arbejde der bliver taget fra bilen på dens tur:

Hvilket vi nu sætte ind i forrige formel og derfra nu finde et udtryk for den højde som bilen i virkeligheden skal op i for at kunne komme igennem loopet:

Hvad man først og fremmest kan se ud fra denne formel er at den ikke er afhængig af massen. Vi lavede først forsøget med en bil med massen 35 gram på en bane med et loop med diameter 2R på 29,5 cm. Dette skulle med den første teori give os en højde h på:

Dette var selvfølgelig ikke nær højt nok til at få bilen hele vejen igennem loopet. Vi prøvede os lidt frem ved at flytte bilen længere og længere op for til sidst at finde den højde hvor den lige præcis kom igennem loopet. (Jeg vil lige gøre opmærksom på at vi behandler bilen som en enkelt partikel, hvorfor højden angiver højden for bilens massemidtpunkt.) Den højde hvor det kunne lade sig gøre at få bilen igennem var 38 cm, hvorfor vores ekstra højde var:

Da vi prøvede at lave forsøget med en bil med en masse på 52 gram fik vi præcist den samme ekstra højde, hvilket stemmer over ens med at denne ikke bør have noget med massen at gøre.
Ud fra denne observation kan vi desuden igen konkludere at gnidningsmodstanden mellem banen og hjulene også er meget lille - da denne jo faktisk er afhængig af massen af bilen (da den er afhængig af den normalkraft som banen påvirker bilen med - som igen er afhængig af den tyngdekraft jorden påvirker bilen med).
Uge 40 - Godkendt logbog
Logbog over øvelse med relativitetsteori
Fysik 1, hold 3, gruppe 4
04.10.2007, torsdag formiddag
Gruppemedlemmer
Johan Jacobsen, Daniel Mulnæs og Pia Jensen.
Vejledning og programmer
Vejledningen kan hentes her, og som LaTEX kildefil her. Første program med synkronisering af ure kan hentes her, andet program med små raketter kan hentes her.
Physlet'erne
- Link til første physlet med ures synkronisering.
- Link til anden physlet med observation af ure.
- Link til tredje physlet med samtidighed for ting der sker på et tog.
- Link til fjerde physlet med rum-tid diagrammer.
Synkronisering af ure
Metode 1:
Det er ikke godt at synkronisere ure på denne måde - den lyspuls der bliver sendt ud har jo en hastighed, hvorfor der vil komme en forsinkelse på de ydre ure i forhold til det inderste.
Det er dog sådan set på denne måde vi gør det i dagligdagen - da lysets hastighed er så stor at vi ikke rigtig kan mærke det...
Metode 2:
Det ER en god måde, da man her tager højde for at lyset har en hastighed, så der kommer ikke den samme forsinkelse på de yderste ure.
Denne metode bruger kun folk der gider bruge penge på det! Det er svært, for man skal opmåle afstanden mellem alle urene før man kan stille dem i forhold til hinanden.
Jeg har lavet et screenshot af VPython programmet med urene, som man kan se ved at klikke på billedet herunder:
Mand der observerer
En mand der står i midten af urene ved det første ur ved metode 1 vil se at alle urene går korrekt, for den forsinkelse de ydre har svarer til den tid det tager for signalet fra dem at vise ham hvad klokken er.
Hvis han står i midten ved metode 2 synes han at de ydre ure er bagud i forhold til uret i midten hvor han står - der er jo en forsinkelse fra disses signaler til at komme ind til ham.
Physlet'en
Metode A:
De synkroniserer urene ved at stille dem alle sammen samtidig i midten og så flytte dem lige så langsomt ud på deres pladser.
Metode B:
De har stillet alle urene ud og målt hvor langt ude de står og korrigeret for at signalet tager noget tid for at komme ud til urene. Dette er en meget hurtigere metode der svarer til metode 2 i VPython programmet.
Sammenligning
Metode A er lige så god som metode B, men den er meget tidskrævende, for urene skal bevæge sig infitisimalt langsomt! Den anden metode er altså langt mere praktisk. Metode B er dog også lidt svær, da man skal foretage nogle afstandsmålinger med ret stor præcision - men i forhold til at bruge en metode hvor urene skal bevæge sig uendelig langsomt så er metode B jo nok bedst.
I virkeligheden bruger vi praktisk nok mest metode A.
Hvis man skal kunne se hvad vi ser i physlet'en skal vi stå lige ud for midten af den så vi får samme signal fra højre og venstre, vi skal altså stå lige ud for uret i midten og se ind på systemet. Dette vil dog bare gøre at uanset hvad vi gør så vil det kun være urene der har samme afstand til os som viser samme tid tilsyneladende for os - der er jo en forsinkelse på visningen af tiden når vi ser på den!
Tog og samtidighed
Først så vi på en physlet der viste hvordan ting kan eller ikke kan være samtidige afhængigt af hvilket inertialsystem man er i.
Derefter så vi på et VPython program med tre raketter der bevægede sig i forhold til hinanden og udsendte lyspulser - hvor man kunne se at der var en forsinkelse på modtagelsen af signalerne. Her er det vigtigt at bemærke at C og B rejser deres flag op når de har fået en lyspuls fra A, mens A rejser sit flag op når hun mener at de andre har fået den - altså efter 100 tidsenheder. Dette er nemt at se når de tre raketter ikke har nogen hastighed i forhold til observatøren, men hvis de har en høj hastighed skal man tage højde for at A mener der er gået 100 sekunder lang tid efter (en gammafaktor efter) observatøren tror de er gået.
Rumtidsdiagrammer
Til sidst så vi på rumtidsdiagrammer i en physlet der viste hvordan en dame gik rundt med hastigheder tæt på lyset.
Uge 41 - Godkendt logbog
Logbog over øvelse 2 med relativitetsteori
Fysik 1, hold 3, gruppe 4
11.10.2007, torsdag formiddag
Gruppemedlemmer
Theis Løye Skafte, Evan James Shymko og Pia Jensen.
Vejledning og programmer
Den udleverede vejledning kan hentes her og som LaTEX kildefil her.
Physlet'er og kode
- Link til paradokset om pælen og laden.
- Link til illustration af et lysur og tidsforlængelsen.
- Download VPython koden til tvillingeparadokset.
- Link rumtidsdiagram over tvillingeparadokset.
Specielt denne gang
Jeg blev af Ian Bearden sat til at lege med programmet RTR (Real Time Relativity) i stedet for at følge det normale skema denne gang - derfor vil jeg bare lige hurtigt gennemgå hvad jeg selv lige er gået igennem ved at følge vejledningen (jeg ville jo ikke gå glip af noget). Efter denne gangs logbog gennemgår jeg lige hvad jeg lavede med RTR i øvelsestiden.
Paradokset om pælen og laden (the barn/pole paradox)
Her så man på en pæl der fløj igennem en lade, set fra ladens og pælens referencesystemer. Man skal så svare på nogle spørgsmål der er givet på siden med physletten.
Fra ladens referencesystem
- a. How fast is the pole moving relative to the barn (measured in c)?
- Dette kan man finde ud af ved at kende hvor lang stangen er i sit
hvilesystem (systemet med hastigheden
 i forhold til
laden) og hvor lang den er når man ser den i ladens referencesystem. Hvilelængden
i forhold til
laden) og hvor lang den er når man ser den i ladens referencesystem. Hvilelængden
 forholder sig til længden
forholder sig til længden  i ladens referencesystem ved følgende formel:
Eftersom længden af stangen i ladens hvilesystem er 10 m og man kan se at længden af den i dens eget hvilesystem er 20 m får jeg altså en gammafaktor på 2, hvorfor hastigheden kan findes på følgende måde:
i ladens referencesystem ved følgende formel:
Eftersom længden af stangen i ladens hvilesystem er 10 m og man kan se at længden af den i dens eget hvilesystem er 20 m får jeg altså en gammafaktor på 2, hvorfor hastigheden kan findes på følgende måde: Og jeg har altså fundet hastigheden
Og jeg har altså fundet hastigheden
 for pælen i
forhold til laden.
for pælen i
forhold til laden.
- Dette kan man finde ud af ved at kende hvor lang stangen er i sit
hvilesystem (systemet med hastigheden
- b. What is 1/slope of the red and green worldlines, respectively?
- Hældningen på en verdenslinie er givet ved c/v, derfor er den
reciprokke værdi af denne givet ved v/c, altså hastigheden på objektet divideret
med c. Derfor er 1/slope det samme som
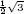 i dette referencesystem.
i dette referencesystem.
- Hældningen på en verdenslinie er givet ved c/v, derfor er den
reciprokke værdi af denne givet ved v/c, altså hastigheden på objektet divideret
med c. Derfor er 1/slope det samme som
- c. What do events A, B, A', and B' refer to? Which if any of these events are
simultaneous in this reference frame?
- A: Forreste ende af pælen kommer ind igennem ladens venstre side.
- B: Bagerste ende af pælen kommer ind igennem ladens venstre side.
- A': Forreste ende af pælen kommer ud igennem ladens højre side.
- B': Bagerste ende af pælen kommer ud igennem ladens højre side.
- B og A' er samtidige i det referencesystem jeg ser på laden i, som jeg går ud fra er lige ud for midten af laden (da definitionen på samtidighed er at to ting er samtidige når de ses som skeende samtidig med samme afstand).
Fra pælens referencesystem
- d. How fast is the barn moving relative to the pole (measured in c)?
- Den må have samme hastighed som pælen havde i forhold til laden,
altså igen
 .
.
- Den må have samme hastighed som pælen havde i forhold til laden,
altså igen
- e. How long is the pole in this reference frame? Why is it this long?
- I dette referencesystem er pælen 20 meter lang, og dette er pælens hvilelængde - eftersom den ligger stille i dette inertialsystem.
- f. How long is the barn in this reference frame? Why is it this long?
- Laden har her en længde på 5 meter, da gammafaktoren selvfølgelig
stadig er 2 (den indbyrdes hastighed mellem laden og pælen er den samme i pælens
hvilesystem som i ladens hvilesystem). I ladens hvilesystem var denne 10 meter
lang, og den er altså nu de fem, eftersom:

- Laden har her en længde på 5 meter, da gammafaktoren selvfølgelig
stadig er 2 (den indbyrdes hastighed mellem laden og pælen er den samme i pælens
hvilesystem som i ladens hvilesystem). I ladens hvilesystem var denne 10 meter
lang, og den er altså nu de fem, eftersom:
- g. What do events A, B, A', and B' refer to? Which if any of these events are
simultaneous in this reference frame?
- A : Forenden af pælen kommer ind igennem ladens venstre side.
- B : Bagenenden af pælen kommer ind igennem ladens venstre side.
- A': Forenden af pælen kommer ud igennem ladens højre side.
- B': Bagenenden af pælen kommer ud igennem ladens højre side.
- Ingen af disse fire begivenheder sker samtidigt når man er i pælens hvilesystem, hvilket er logisk eftersom laden og pælen skal være lige lange i det benyttede referencesystem for at dette kan forekomme (hvilket de jo netop er i ladens referencesystem).
Lysure
Her skal man se på hvordan tiden går for et objekt der bevæger sig, her et ur der måler tiden ved hjælp af lyspulser.
- Note that the light clock reads time in "stationary" meters (i.e. meters traveled in
a stationary clock). Why can we do this? In other words, how is the conversion
accomplished and what does it depend on? Compute the time interval between successive ticks.
- Der sker kun længdeforkortelse i bevægelsesretningen, hvilket her er x-retningen. I y-retningen sker der altså intet med længden, og det er netop højden af uret vi ser på når vi måler tiden - derfor kan man gøre det.
- Tidsintervallet vil være givet ved afstanden rejst med hastigheden af lyspulsen,
hvorfor tiden altså er givet ved:
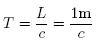
- Given Einstein's postulate about the constancy of the speed of light, what can we say
about the ticking of the moving clock (as seen by the stationary observer) relative to the
ticking of the stationary clock?
- Eftersom lyset i det bevægede ur skal rejse et længere stykke, vil tiden nødvendigvis gå langsommere i det bevægede ur, da hastigheden jo altid er den samme for lys.
- Show that the light travel time
 as observed
from the stationary frame is given by the following expression:
as observed
from the stationary frame is given by the following expression:

- Dette er sådan set en direkte følge af Pythagoras' læresætning for en retvinklet
trekant. Jeg ved at den samlede afstand lyspulsen her rejst er kvadratet af venstresiden
af ligningen (denne er hypotenusen i trekanten), og at lyspulsen i y-retningen har rejst
længden
 , mens den i x-retningen har rejst længden
, mens den i x-retningen har rejst længden
 , derfor vil Pythagoras' sige at de to retninger
i anden potens lagt sammen MÅ være den kvadrerede længde af hypotenusen.
, derfor vil Pythagoras' sige at de to retninger
i anden potens lagt sammen MÅ være den kvadrerede længde af hypotenusen.
- Dette er sådan set en direkte følge af Pythagoras' læresætning for en retvinklet
trekant. Jeg ved at den samlede afstand lyspulsen her rejst er kvadratet af venstresiden
af ligningen (denne er hypotenusen i trekanten), og at lyspulsen i y-retningen har rejst
længden
- How fast must the moving clock travel to tick at one half the rate of the stationary clock?
- Dette kan jeg finde ud af direkte ved hjælp af tidsforlængelse. Jeg får sammenhængen:
Og jeg har altså fundet hastigheden som uret skal bevæge sig med for at tiden går med den halve tid i forhold til tiden på det stillestående ur. Efter at have tjekket ved indsættelse af værdien (0.866 c) i animationen kunne jeg også se at dette var korrekt.

- Dette kan jeg finde ud af direkte ved hjælp af tidsforlængelse. Jeg får sammenhængen:
- Along the axis of motion, how long is the moving clock (as seen from the stationary frame)
relative to the length of the stationary clock? Why is this modification necessary? In other
words, if the length of the moving clock were unchanged, would we get consistent results?
- Hvilelængden
 af uret (i x-aksens retning) er en halv
meter, og uret bevæger sig med en hastighed
af uret (i x-aksens retning) er en halv
meter, og uret bevæger sig med en hastighed  på
på
 . Jeg bruger så formlen for længdeforkortelse og
isolerer
. Jeg bruger så formlen for længdeforkortelse og
isolerer  (længden af det bevægede ur set i det
stationæres hvilesystem). Jeg får denne til at være:
Hvis længden af uret ikke ændrer sig på denne måde så ville tiden gå hurtigere for det bevægede ur set fra det stillestående.
(længden af det bevægede ur set i det
stationæres hvilesystem). Jeg får denne til at være:
Hvis længden af uret ikke ændrer sig på denne måde så ville tiden gå hurtigere for det bevægede ur set fra det stillestående.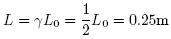
- Hvilelængden
Ud over spørgsmålene givet ved physlet'en fik vi også et par spørgsmål i vejledningen, som jeg her har givet svar på:
- At the bottom of the page, there is an explanation of why a clock parallel to the direction
of motion must measure the same result as the previous clock (and the one in your textbook). Do
you agree with the explanation given? Can you (whether or not you agree) give another explanation?
- Der står at den nødvendige effekt er længdeforkortelseen. Når denne gør uret kortere vil uret gå ligeså hurtigt som det lodrette ur med den samme hastighed. Det går derfor op med at tiden går en gammafaktor langsommere i begge tilfælde.
- Does this demonstration help you make sense of the traveling rocket simulation from last week?
- I sidste uge legede vi med programmet "relativistic rockets", hvor der var 3 raketter - hver med et flag. Alle tre raketter bevægede sig med samme hastighed. Alice starter med at udsende et signal med lysets hastighed, og udregner at det vil tage signalet 100 sekunder at nå hen til de andre skibe, der er lige langt væk i hvilesystemet hvor alle tre rumskibe står stille. Alice hejser sit flag når hun tror de andre har fået signalet, altså 100 sekunder efter hun har sendt signalet af sted, men når de bevæger sig i forhold til vores intertial system vil Alice jo have en tidsforsinkelse (med en gammafaktor). Derfor går der mere end de 100 sekunder før hun hejser flaget.
Tvillingeparadokset
Her så vi på VPython programmet twins.py (hent det her). Dette program viser hvordan to tvillinger rejser fra hinanden - den ene tvilling bliver hjemme på jorden, mens den anden, Alice, tager en tur til Alpha Centauri og tilbage igen. Jeg vil her svare på de givne spørgsmål:
- What do the white and yellow rings represent?
- De hvide ringe udsendes af tvillingen på jorden hver gang der er gået et år for denne i dennes eget hvilesystem. De gule ringe udsendes af Alice når der i hendes hvilesystem er gået et år.
- How much time elapses between white rings and how much between yellow? How does this change with
the speed you give the traveling twin's spaceship?
- Hvis der går et år mellem hver hvid lyspuls fra jorden vil der gå et år divideret med gammafaktoren mellem hver af de gule lyspulser fra Alice. Så jo mere fart Alice har på, des længere tid går der mellem de gule lyspulser i forhold til de hvide.
- How much energy would it take to give a spaceship of 10,000 kg a speed of 0.8 c?
- Jeg skal her se på den kinetiske energi som raketten har ved denne hastighed, denne energi
må være den energi som der skal tilføres rumskibet for at accelerere op på denne hastighed, hvis
altså jeg ignorerer luftmodstand i starten og diverse andre sjove ting. Denne energi er altså
givet ved:
Dette er VIRKELIG meget energi!

- Jeg skal her se på den kinetiske energi som raketten har ved denne hastighed, denne energi
må være den energi som der skal tilføres rumskibet for at accelerere op på denne hastighed, hvis
altså jeg ignorerer luftmodstand i starten og diverse andre sjove ting. Denne energi er altså
givet ved:
- If the twins start at birth, and the traveling twin should be home in time for her twin's funeral
(assuming the stay-at-home-twin lives the average lifespan), how fast must her spaceship travel?
- Jeg går ud fra at tvillingen der bliver hjemme bliver omkring 80 år gammel. Dette betyder at
 er omkring
er omkring  . Afstanden til
Alpha Centauri er
. Afstanden til
Alpha Centauri er  - og denne afstand skal Alice altså
tilbagelægge to gange på tiden
- og denne afstand skal Alice altså
tilbagelægge to gange på tiden  for at hun når hjem på det
rigtige tidspunkt. Dette svarer til hastigheden:
for at hun når hjem på det
rigtige tidspunkt. Dette svarer til hastigheden:

- Jeg går ud fra at tvillingen der bliver hjemme bliver omkring 80 år gammel. Dette betyder at
- How much energy would this take?
- En hastighed på 0.110 c ville kræve følgende energi:
Hvis jeg da går ud fra at Alices rumskib ikke sænker farten på noget tidspunkt på rejsen og ikke bruger noget energi på at vende om når det er fremme ved Alpha Centauri.

- En hastighed på 0.110 c ville kræve følgende energi:
- What implications does this have for near term interstellar travel?
- Dette er en fuldkommen ekstrem mængde energi at bruge på en rejse. Hvis man nu for eksempel
får sin energi fra antistof (ligesom i Star Trek) skal man bruge følgende masse antistof:
Dette er i sig selv ikke så meget for et 10 tons stort rumskib, men i og med at CERN bruger et minut på at lave omkring 50 mio. antiprotoner kommer det til at tage ekstremt lang tid at lave denne masse antistof, og så vil det for den sags skyld også være ekstremt svært at opbevare!

- Oven i købet må det jo være sådan at Alice skal bruge denne energi på at komme op i fart, derefter igen på at bremse ned, så for at komme op i fart igen for til sidst at bremse ned endnu engang - hvilket bare gør tallet endnu større.
- Dette er en fuldkommen ekstrem mængde energi at bruge på en rejse. Hvis man nu for eksempel
får sin energi fra antistof (ligesom i Star Trek) skal man bruge følgende masse antistof:
- Which twin would you rather be?
- Altså vægtløshed ville jo være sejt, men jeg har ikke lyst til at sidde i et rumskib i så lang tid, og for den sags skyld er den acceleration som skibet skal have for tilnærmelsesvist at komme op på så store hastigheder nok ikke behagelig, trods det faktum at skibet har et ret langt stykke at accelerere på (man vil jo gerne op i høj fart hurtigst muligt).
Rumtidsdiagram over tvillingeparadokset
Til sidst skulle vi se på et rumtidsdiagram over paradokset med tvillingerne. Denne physlet skulle vi bare kigge lidt på og se hvad det egentlig var der skete.
Når man ser lyspulserne fra den tilbageblivne tvillings hvilesystem så ser det på udrejsen ud
til at lyspulserne kommer med en frekvens på en gammafaktor mere end et år, på hjemrejsen er det
en gammafaktor mindre (altså divideret med gamma i stedet for ganget med).
Hvad der er værd at lægge mærke til i denne physlet er den sidste af de tre dele man kan vælge.
Her ser man hvad det egentlig er den tilbageblevne tvilling ser, og altså ikke hvad der virkelig
sker.
Uge 41 - Godkendt logbog, ekstra-leg med RTR
Logbog over eksperimenteren med relativitetsteorisimulator
Jeg har leget lidt med et program der hedder RTR - Real Time Relativity 0.8 - lavet af Lachlan McCalman og Antony Searle fra The Australian National University. Jeg vil herunder lige opliste nogle relevante links:
- Hjemmesiden for programmet.
- Download af programmet version 0.8 (released 27. August 2007), læg mærke til at programmet kun kan køre på Windows og at det kræver en programmerbar GPU.
- Manualen til programmet.
- Lab-manual til en øvelse på The Australian National University.
Programmet
I programmet kan man "flyve" rundt i et lille rumskib der kan komme op på hastigheden 0.999c. Her kan man så se hvordan verden ville se ud hvis man virkelig sad i sådan et rumskib. Man kan først og fremmest se hvordan vinkler og afstande ændrer sig, og eftersom der er opstillet en række af ure på "banen" kan man også se hvordan tiden ændrer sig. I øverste venstre hjørne af displayet kan man se hvilken hastighed man har samt hvad tiden i sit eget og i banens inertialsystem er. Desuden kan man se placeringen af kameraet.
Hvad kan det bruges til?
Dopplereffekten og Headlight Effect
I programmet kan man desuden slå dopplereffekten til og fra. Når man bevæger sig mod noget
med en hastighed vil det lys man ser umiddelbart få ændret sin frekvens - hvis man er på vej
mod en lyskilde vil man se flere bølger end hvis man stod stille, og det modsatte hvis man er
på vej væk fra lyskilden. Den frekvens  som jeg ser i rumskibet
med en hastighed
som jeg ser i rumskibet
med en hastighed  er givet ved den udsendte frekvens
er givet ved den udsendte frekvens
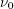 og vinkelen
og vinkelen  mellem det
indkomne lys og hastigheden ved sammenhængen:
mellem det
indkomne lys og hastigheden ved sammenhængen:

Dette betyder at når jeg bevæger mig mod en lyskilde vil dens lys blive blåforskudt, og jeg vil se den som værende mere blå des mere hastighed jeg får på. Bevæger jeg mig væk fra en lyskilde vil jeg så se en rødforskydning. I programmet kan man se dette på to forskellige måder - der er altså for forskellige modes man kan se dopplereffekten på. Forskellen på de to er sådan set bare hvor høj en hastighed man kan få på uden at alt bliver helt sort (ultraviolet). Jeg har ikke nået at finde så stor forskel på dem dog.
I programmet er der også en effekt de kalder for Headlight Effect. Når man rejser med høj hastighed vil man opfange flere fotoner i hastighedens retning end den anden vej, hvorfor det man ser vil være lysere foran og mørkere når man ser sig tilbage. Jeg har, hvis man klikker på billedet herunder, vist hvordan skærmen ser ud når man har slået både Headlight Effect og dopplereffekten til og flyver med en hastighed på 0.923 c:
Man kan her tydeligt se hvordan midten af skærmen er totalt hvid fordi der er så høj fart på - hvorfor Headlight effekten gør at man opfanger langt flere fotoner i dette område. Desuden kan man se at hele billedet er i gråtoner - hvilket i virkeligheden nok ville være tæt på sort i stedet - dette skyldes dopplereffekten der gør at alt det lys der ses er forskudt helt ind i det ultraviolette område.
Samtidighed
På banen er der opstillet fem ure som man kan lege med samtidighed med. Der er i selve programmet to forskellige genvejstaster, C og I, hvor man med den første kommer til at flyve med 0.5 c parallelt med urene - og man med den anden kommer til at slå helt stille og så ind på det midterste ur. Jeg har taget et screenshot af det sidste, som vises ved at klikke på billedet herunder:
Man kan på billedet se at tiden på urene ved siden af midteruret er et sekund bagud, mens urene yderst er to sekunder bagud. Dette skyldes at lyset fra urene (med informationen om hvad uret viser) skal bruge mere tid på at komme til observatøren end lyset for uret i midten skal for at komme samme sted hen.
Hvad jeg har opdaget
Når man flyver med høj hastighed mod en lige flade vil det virke som om at denne flade buer væk fra en - så den faktisk ligner en kugle mere og mere jo tættere på lyshastigheden man er. Jeg har taget et screenshot af dette fænomen, som er at se ved at klikke på billedet herunder:
Den overflade som man ser her er faktisk helt flad, men jeg bevæger mig imod den med en hastighed på 0.931 c, hvorfor den virker til at bue, da det punkt der har kortest afstand til mig (lige foran mig) også har kortest afstand for lyset fra overfladen til mig. Lyset fra kanterne af fladen skal rejse længere for at jeg ser det - hvorfor jeg ser det med en "forsinkelse" der gør at jeg tror kanterne er længere væk fra mig. Dette danner en kugleeffekt som set.
Uge 42 - Godkendt logbog
Logbog over øvelse med dopplereffekt og partikelhenfald
Fysik 1, hold 3, gruppe 4
25.10.2007, torsdag formiddag
Gruppemedlemmer
Daniel Green Hersing, Christopher Gerlach og Pia Jensen.
Vejledning og programmer
Den udleverede vejledning kan hentes her og som LaTEX kildefil her.
Tvillingeparadokset igen
Først skulle vi se på det program vi arbejdede med sidste gang med tvillingeparadokset. Dette er at hente her.
Relativistisk kinetisk energi
Vi skulle først se på forskellen mellem kinetisk energi når man arbejder klassisk og når man arbejder relativistisk. Dette skulle vi så tegne i en graf over de to overfor hinanden for at se hvordan og hvornår de begynder at blive forskellige. Vi valgte at lave en graf i 3 dimensioner, hvor vi kunne definere den kinetiske energi som en funktion af to variable, nemlig massen og hastigheden. Herunder viser jeg vores graf (som man hente i større format som pdf ved at klikke på den):
Det er tydeligt at se hvordan energien relativistisk (den af graferne der ændrer sig drastisk opad mod uendelig når hastigheden bliver tæt på lysets) ændrer sig til at være meget højere end den klassiske for høje hastigheder (hvor hastigheden på grafen er givet som
 , altså hastigheden divideret med lyshastigheden
, altså hastigheden divideret med lyshastigheden
 ).
).
De to grafer er lavet over de to funktioner som følger:

 på en af akserne i stedet for hastigheden
på en af akserne i stedet for hastigheden
 . Men hensyn til hvornår de to grafer begynder virkelig
at skille sig fra hinanden vurderer jeg at dette sker for en hastighed på omkring 0.3-0.4
. Men hensyn til hvornår de to grafer begynder virkelig
at skille sig fra hinanden vurderer jeg at dette sker for en hastighed på omkring 0.3-0.4
 , hvor forskellen på de to er cirka 1 %.
, hvor forskellen på de to er cirka 1 %.
Man kan ikke ligefrem sige at videnen om den relativistiske kinetiske energi gør det tilsyneladende nemmere for aliens at komme hertil - grafen viser tydeligt at jo tættere på lysets hastighed du vil, des mere energi skal der til for at du kan komme til at accelerere derop, hvorfor det også er umuligt at komme op på den hastighed som lyset rent faktisk har. Så med hensyn til sandsynligheden for at aliens besøger trailerparker i Mississippi er den for nedadgående med denne viden om relativistisk kinetisk energi.
Frekvens af Alice's signal
Efter at have overvejet dette skulle vi så gå videre til at aflæse den frekvens som
den hjemmeblivende tvilling målte af det signal som Alice udsendte. Alice udsendte vel
og mærke et signal en gang om året i sit eget hvilesystem, men dette signal vil ikke have
samme frekvens set fra andre systemer der ikke er i hvile i forhold til hende. Vi tog en
række "målinger" ud fra programmet for at kunne regne os frem til den frekvens hvormed
tvillingen hjemme på jorden så signalerne fra Alice. Disse har jeg listet op herunder
(hvilket vel og mærke er for rumskibet når det har en hastighed på 0.5
 ):
):
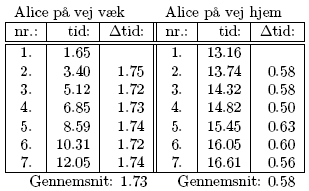
Dette er vel og mærke ikke egentlige punkter, men aflæsninger af hvornår bølgen fra Alice rammer jorden. Vi har fundet gennemsnittet af frekvensen simpelthen for at finde den frekvens som virker til at være den der giver mest mening.
Efter at have udregnet denne frekvens skulle vi kommentere om den nu også var realistisk.
Dette kan vi gøre ved hjælp af den relativistiske dopplerforskydning, der siger at

 = -0.5 og
= -0.5 og
 = 1 for udturen og værdierne
= 1 for udturen og værdierne
 = 0.5 og
= 0.5 og  = 1 for
hjemturen, fik vi værdierne
= 1 for
hjemturen, fik vi værdierne  = 1.732 og
= 1.732 og
 = 0.577 for henholdsvis turen ud og hjem. Dette passer
godt på vores "målinger", hvorfor disse da må være ret realistiske.
= 0.577 for henholdsvis turen ud og hjem. Dette passer
godt på vores "målinger", hvorfor disse da må være ret realistiske.
Nummerplade
Til sidst skulle vi svare på om en nummerplade (bag på en bil) var logisk med påskriften BLUESHFT. Problemet med denne nummerplade er at den nok skal imponere over at bilen bliver blåforskudt fordi den kører så hurtigt - eneste minus er at hvis noget bevæger sig væk fra en, så bliver det rødforskudt, hvorfor bilen kun bliver blåforskudt hvis den er på vej MOD en. Her skal man så lige huske at bilen kun havde nummerpladen i bagenden, altså bliver den kun blåforskudt hvis enten dag bagvedkørende kører hurtigere end den pågældende bil, eller hvis bilen er en eller anden underlig bil der bakker hele tiden!
Partikelhenfald
Urankernes henfald
Vi skulle herefter gå ind og se på følgende physlet omkring henfald af en urankerne: Link.
Her skulle vi svare på et par spørgsmål, som jeg har oplistet herunder:
- What is the mass of the parent nucleus?
- Denne kunne vi slå op i en ganske normal databog til at være 238.050785 atommasseenheder (u).
- What is the daughter nucleus? What is its mass?
- Datterkernen er en thorium-234 kerne, og dennes masse fandt vi på samme måde til at være 234.043593 atommasseenheder.
- What is the mass of the alpha particle?
- Igen slog vi op i en databog, og fandt denne til at være 4,00260324 atommasseenheder.
- How much mass is converted into energy? What is the resulting energy?
- Dette finder man simpelthen ved at vi kender sammenhængen mellem masse og energi til at
være:
Hvorfor vi bare kan udregne ændringen af masse. Dette bliver:
 Hvilket altså svarer til energien:
Hvilket altså svarer til energien: Dette er altså den energi der bliver frigivet under henfaldet af moderkernen til datterkernen og alfapartiklen. Omregnet er dette en energi på
Dette er altså den energi der bliver frigivet under henfaldet af moderkernen til datterkernen og alfapartiklen. Omregnet er dette en energi på
 .
.
- Dette finder man simpelthen ved at vi kender sammenhængen mellem masse og energi til at
være:
- Can you measure the speed of the alpha particle to determine its energy?
- Vi kan aflæse af alfapartiklen bevæger sig 17 tern på 1.2 mikrosekunder, hvilket vi kan
omregne da vi ved at et tern er cirka en meter og at en tidsenhed er et mikrosekund. Dette
bliver til en hastighed på:
Hvilket svarer til den kinetiske energi:
 Som omregnet er en energi på
Som omregnet er en energi på
 .
.
- Vi kan aflæse af alfapartiklen bevæger sig 17 tern på 1.2 mikrosekunder, hvilket vi kan
omregne da vi ved at et tern er cirka en meter og at en tidsenhed er et mikrosekund. Dette
bliver til en hastighed på:
- Do these two energies agree? Why or why not?
- Denne energi er næsten den samme som den energi der samlet blev frigivet under henfaldet,
hvorfor jeg også lige vil se på hvor meget energi datterkernen får:
Vi kan aflæse at den store partikel bevæger sig seks tern på 16 mikrosekunder. Dette svarer til en hastighed på:og en kinetisk energi på: Som omregnet er en energi på
Som omregnet er en energi på
 . Disse to kinetiske energier
giver sammenlagt næsten den energi der bliver frigivet under henfaldet, hvorfor jeg må sige
at energien er bevaret og at dette derfor giver mening (dog er dette med en ret stor
fejlmargin, set i forhold til at det sådan set burde være 100 % korrekt det jeg finder -
det er jo et PROGRAM jeg arbejder med, ikke normale målinger der har usikkerheder).
. Disse to kinetiske energier
giver sammenlagt næsten den energi der bliver frigivet under henfaldet, hvorfor jeg må sige
at energien er bevaret og at dette derfor giver mening (dog er dette med en ret stor
fejlmargin, set i forhold til at det sådan set burde være 100 % korrekt det jeg finder -
det er jo et PROGRAM jeg arbejder med, ikke normale målinger der har usikkerheder).
- Denne energi er næsten den samme som den energi der samlet blev frigivet under henfaldet,
hvorfor jeg også lige vil se på hvor meget energi datterkernen får:
Ud over disse spørgsmål skulle vi svare på hvilken referanceramme vi så på forsøget fra, center-of-mass systemet eller laboratoriesystemet. Ser vi klassisk på henfaldet vil center-of-mass systemet og laboratoriesystemet her være det samme, men relativistisk burde vi, hvis vi var i center-of-mass systemet, følge lidt med alfapartiklen mod venstre eftersom denne får en større masse på grund af sin store hastighed (og at energi, her kinetisk, jo svarer til masse). Så alt i alt er vi i et laboratoriesystem.
K-mesoners henfald til to pioner
Herefter skulle vi så så på en ny physlet omkring henfaldet af en specificerbar partikel: Link. Her kunne man altså selv vælge massen og hastigheden af moderkernen samt massen af de to kerne der kom ud af spaltningen.
Her skulle vi først se på henfaldet hvor en K-meson med en hastighed vi selv bestemte og med
massen  og henfaldt til to pioner hver med massen
og henfaldt til to pioner hver med massen
 . Vi skulle så svare på nogle spørgsmål:
. Vi skulle så svare på nogle spørgsmål:
- From what reference frame are you viewing the decay?
- Vi ser henfaldet i et laboratoriesystem.
- How would the decay look if you were in the Kaons reference frame?
- Hvis vi fulgte K-mesonen i dens eget hvilesystem ville denne selvfølgelig være i hvile. Når den så henfalder til de to pioner vil det i dette referencesystem virke som om at de to datterpartikler fjerner sig med lige stor fart i diametralt modsatte retninger (egentlig er det den samme impuls, men da de to datterpartikler har samme masse betyder dette også samme fart).
- In the simulation, the two decay products are always emitted parallel to the direction of the
mother particle’s motion. Is this realistic?
- Dette er ikke spor realistisk nej. Så længe impulsbevarelsen er overholdt kan de to datterpartikler flyve i hvilken som helst retning i rumme som de har lyst til, så længe de hele tiden har en indbyrdes vinkel på 180 grader i forhold til hinanden (altså igen, diametralt modsatte retninger).
Lambdapartikels henfald og tidsforlængelse
Til sidst skulle vi se på en Lambda-partikel der henfaldt. Denne har en levetid på cirka 0.26 ps, og henfalder cirka 2/3 af gangende til en proton og en pion. Vi skulle ved at argumentere ved dette henfald se om physlet'en tog hensyn til tidsforlængelse.
For at kunne gøre dette satte hastigheden til 0.1  og 0.9
og 0.9
 og så på placeringen og tiden for et henfald. Partiklen
henfaldt på samme tidspunkt og samme sted ved begge hastigheder i physlet'en, hvorfor det er
tydeligt at den ikke tager højde for tidsforlængelse. Hvis den havde gjort dette ville der gå
længere tid for Lambda-partiklen at henfalde (tid er vel og mærke i laboratoriesystemet) hvis
den havde en højere hastighed.
og så på placeringen og tiden for et henfald. Partiklen
henfaldt på samme tidspunkt og samme sted ved begge hastigheder i physlet'en, hvorfor det er
tydeligt at den ikke tager højde for tidsforlængelse. Hvis den havde gjort dette ville der gå
længere tid for Lambda-partiklen at henfalde (tid er vel og mærke i laboratoriesystemet) hvis
den havde en højere hastighed.







